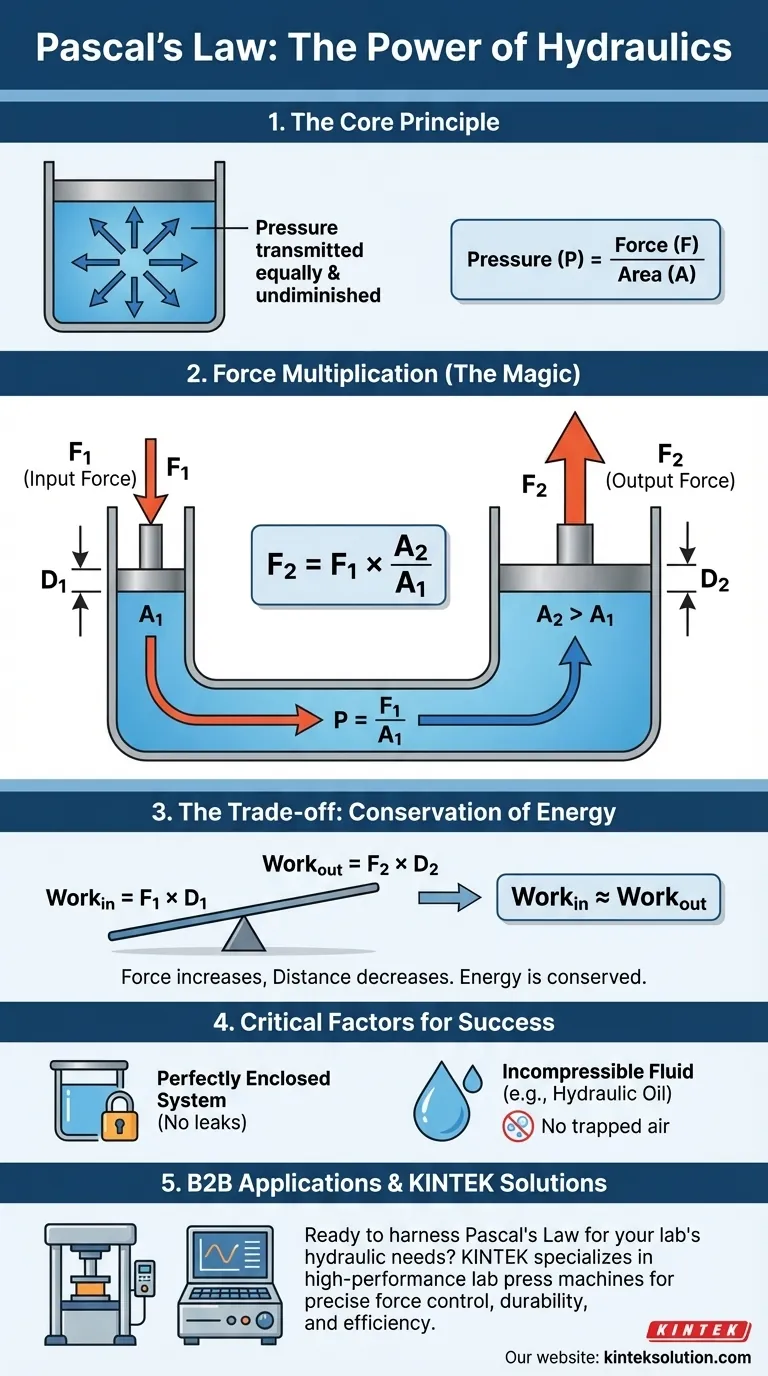
По своей сути, закон Паскаля гласит, что изменение давления в любой точке замкнутой, несжимаемой жидкости передается одинаково и без потерь во все части этой жидкости. Это означает, что если вы давите на жидкость в герметичном контейнере, давление во всем контейнере увеличивается на одну и ту же величину, в одно и то же время.
Хотя определение сосредоточено на передаче давления, истинная сила закона Паскаля заключается в том, как он позволяет нам достигать массивного умножения силы. Этот единственный принцип является основой почти всех современных гидравлических систем.
Основное уравнение: Давление, Сила и Площадь
Чтобы понять последствия закона Паскаля, вы должны сначала понять взаимосвязь между его тремя основными компонентами.
Определение давления
Давление (P) определяется как Сила (F), приложенная к определенной Площади (A). Уравнение: P = F/A.
Подумайте о разнице между тем, когда кто-то толкает вас открытой ладонью, и когда толкает одним пальцем. Сила может быть одинаковой, но давление от кончика пальца намного больше, потому что оно сосредоточено на гораздо меньшей площади.
Роль несжимаемой жидкости
Закон Паскаля основан на использовании несжимаемой жидкости, такой как вода или гидравлическое масло. Когда вы прилагаете силу к этому типу жидкости, она не сжимается до меньшего объема.
Поскольку жидкость не может быть сжата, энергия, которую вы вводите, должна передаваться в другое место. Именно так давление мгновенно распространяется по всей системе.
Магия умножения силы
Истинный гений применения закона Паскаля заключается не только в том, что давление передается, но и в том, что его можно использовать для умножения силы. Это рабочий принцип, лежащий в основе всего, от автомобильного домкрата до шасси самолета.
Базовая гидравлическая модель
Представьте себе U-образную трубку, заполненную маслом, запечатанную с обоих концов поршнями. Один поршень маленький (входной поршень), а другой большой (выходной поршень).
Приложение входной силы
Допустим, вы прилагаете небольшую силу вниз (F1) к малому поршню, площадь которого равна A1. Это создает давление в жидкости: P = F1 / A1.
Передача давления
Согласно закону Паскаля, это точное давление (P) теперь присутствует везде в жидкости. Это включает в себя область непосредственно под большим выходным поршнем.
Расчет выходной силы
Это же давление (P) теперь давит вверх на большой поршень, площадь которого равна A2. Результирующая сила вверх (F2) равна F2 = P × A2.
Поскольку давление одинаково во всем (F1/A1 = F2/A2), вы можете видеть, что выходная сила пропорциональна соотношению площадей. Если площадь выходного поршня в 10 раз больше площади входного поршня, выходная сила будет в 10 раз больше приложенной вами силы.
Понимание компромиссов
Это умножение силы не берется из ниоткуда; оно подчиняется законам физики и включает в себя критические компромиссы.
Закон сохранения энергии
Вы не можете создавать энергию из ничего. Хотя выходная сила умножается, расстояние, на которое перемещается выходной поршень, пропорционально уменьшается.
Чтобы поднять большой поршень на 1 дюйм, вам может потребоваться опустить малый поршень на 10 дюймов. Работа (Сила × Расстояние) остается одинаковой с обеих сторон, если не учитывать трение.
Важность "замкнутой" системы
Принцип Паскаля работает только в идеально герметичной системе. Любая утечка приведет к вытеканию жидкости при приложении давления, рассеивая давление и приводя к сбою системы.
Свойства жидкости имеют значение
Хотя мы часто предполагаем идеальную, несжимаемую жидкость, гидравлические жидкости в реальном мире обладают вязкостью (сопротивлением потоку) и могут содержать захваченные пузырьки воздуха. Воздух сильно сжимаем, и его присутствие в гидравлических линиях может сделать систему "губчатой" и резко снизить ее эффективность.
Как применить это к вашему проекту
Понимание этого принципа позволяет эффективно проектировать системы и устранять неисправности. Ваша конкретная цель будет определять, какой аспект закона является наиболее важным.
- Если ваш основной фокус — механическое преимущество: Сосредоточьтесь на максимальном увеличении соотношения площадей между выходным и входным поршнями (A2/A1) для достижения желаемого умножения силы для пресса или подъемного домкрата.
- Если ваш основной фокус — эффективность системы: Уделите первостепенное внимание созданию идеально герметичной системы и использованию высококачественной, несжимаемой жидкости для минимизации потерь энергии из-за утечек или внутреннего сжатия.
- Если ваш основной фокус — точное управление: Используйте компромисс в работе; небольшое, управляемое движение на входе может преобразоваться в очень маленькое, но мощное и точное движение на выходе, что идеально подходит для таких систем, как автомобильные тормоза.
Понимая этот принцип, вы переходите от простого знания определения к постижению элегантной силы, стоящей за всей гидравлической инженерией.
Сводная таблица:
| Аспект | Ключевое понимание |
|---|---|
| Определение | Изменение давления в несжимаемой жидкости передается одинаково и без потерь. |
| Умножение силы | Выходная сила увеличивается с соотношением площадей (F2 = F1 × (A2/A1)). |
| Компромиссы | Увеличение силы уменьшает расстояние перемещения; энергия сохраняется. |
| Применение | Используется в гидравлических домкратах, прессах и системах точного управления. |
Готовы использовать закон Паскаля для гидравлических нужд вашей лаборатории? KINTEK специализируется на высокопроизводительных лабораторных прессах, включая автоматические лабораторные прессы, изостатические прессы и прессы с подогревом. Наше оборудование обеспечивает точный контроль силы, долговечность и эффективность для ваших лабораторных применений. Свяжитесь с нами сегодня, чтобы обсудить, как наши решения могут оптимизировать ваши проекты и повысить производительность!
Визуальное руководство
Связанные товары
- Автоматический лабораторный гидравлический пресс для прессования гранул XRF и KBR
- Ручной гидравлический лабораторный пресс с подогревом и встроенными горячими плитами Гидравлическая пресс-машина
- Автоматическая гидравлическая пресс-машина с подогревом и горячими плитами для лаборатории
- Автоматическая гидравлическая пресс-машина с подогревом с подогреваемыми плитами для лаборатории
- Лабораторный гидравлический пресс Лабораторный пресс гранулы машина для перчаточного ящика
Люди также спрашивают
- Какие меры безопасности связаны с использованием гидравлических прессов в лабораториях?Обеспечение защиты оператора и оборудования
- Как гидравлический пресс помогает в рентгенофлуоресцентной спектроскопии? Достижение точного элементного анализа с помощью надежной пробоподготовки
- Какова цель создания гранул для рентгенофлуоресцентной спектроскопии с использованием гидравлического пресса? Обеспечение точного и воспроизводимого элементного анализа
- Почему гидравлический пресс важен для ИК-Фурье спектроскопии? Обеспечьте точный анализ образцов с помощью таблеток KBr
- Как гидравлические прессы используются в лабораторной пробоподготовке? Обеспечение точности анализа при использовании однородных образцов
